| Previous | Index | Next |
I have to admit, I'm a little confused at all of the coverage of a recent paper. You can read some of the coverage at these places:
The paper is titled "The first digit frequencies of primes and Riemann zeta zeros tend to uniformity following a size-dependent generalized Benford's law" and was authored by Bartolo Luque and Lucas Lacasa. The key claim in the paper is "Benford's law... describes with astonishing precision the statistical distribution of leading digits in the prime numbers sequence."
There are two key facts to note before we continue:
- The distribution of primes is estimated as x/ln(x).
- Benford's law describes a logarithmic distribution
In other words, of course Benford's law describes the prime distribution. The prime distribution is logarithmic, and Benford's law describes logarithmic distributions.
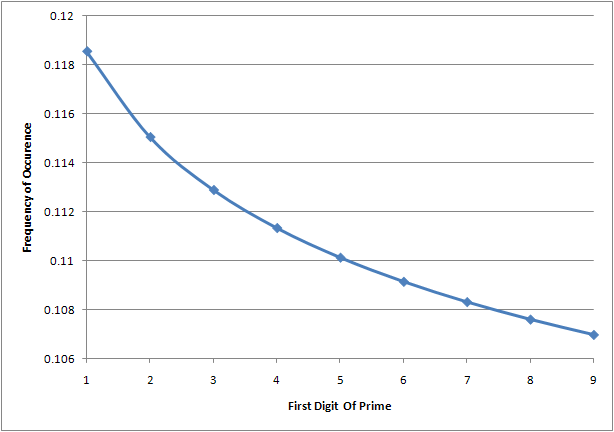
For instance, let's limit ourselves to numbers that are 6 digits long. Here are the estimates for the primes in the following ranges:
100,000 - 200,000 : 7,699 primes that start with "1"200,000 - 300,000 : 7,402 primes that start with "2"300,000 - 400,000 : 7,221 primes that start with "3"400,000 - 500,000 : 7,093 primes that start with "4"500,000 - 600,000 : 6,994 primes that start with "5"600,000 - 700,000 : 6,913 primes that start with "6"700,000 - 800,000 : 6,846 primes that start with "7"800,000 - 900,000 : 6,788 primes that start with "8"900,000 - 1,000,000 : 6,737 primes that start with "9"
Notice how the number of primes keeps decreasing? This is a well understood mathematical property of primes that has been known since the 18th century.
If you work out the frequencies for each digit you'll get a plot like this:
This plot was generated using the prime counting function discovered in the 18th century.
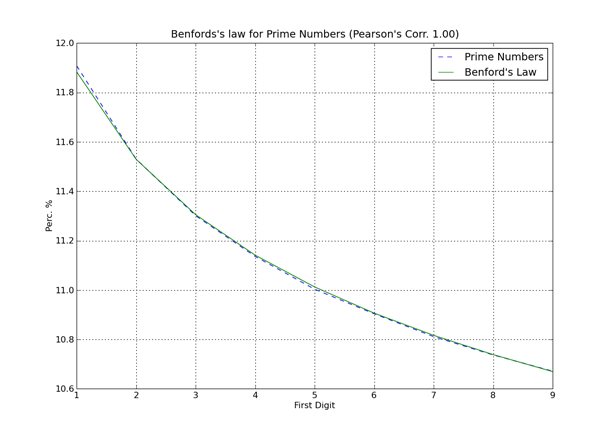
Now compare this to the plot from PyEvolve's write-up about the paper and its significance:
Nothing new to see here.
|
About the author I'm Steve Krenzel, a software engineer and co-founder of Thinkfuse. Contact me at steve@thinkfuse.com. |

|
| Previous | Next |